It’s game day… with a twist.
Games are everywhere, including websites that purport to “train your brain.” Games are employed in divergent thinking tests to “measure” your creativity. As I have argued in earlier blogs, you can use games to train your brain if you want to train your brain to play those games.
Do the brain training games improve your ability to concentrate in learning Mandarin? That’s not been proven. However, in terms of the neuroplasticity of the brain, it’s better to learn Mandarin than to “train” to improve potentially applicable skills.
So, keeping in touch with words by doing the daily crossword puzzle will not help you become a good writer or prevent your writing skills from deteriorating. Only writing can do that. Doing the puzzle is fun, but it is not a stepping stone to higher learning skills. (If you are diagnosed with a cognitive deficit, using your brain in any capacity may help slow deterioration.)
Nonetheless, today is game day with a twist. We are going to solve a child’s puzzle step by step with an eye on identifying transferrable techniques, looking for tools that might help solve more complex problems. Which is problematic, as they say. So, here is today’s game problem:
What is ½ of 8?
Of course, it’s 4. Everyone knows that.
Technique #1: Always begin with the obvious. It’s astonishing how groups of people become stymied because no one wants to say the obvious. No one in the group wants to be the simpleton that says what, supposedly, everyone is already thinking. That’s one way consultants can make a lot of money—they state the obvious, dressed up in fine, frilly terms to justify their fees. So, check the obvious first: is the machine plugged in, does the car have gas and so on. It’s simple, but it can save time, effort, and money.
What else is ½ of 8?
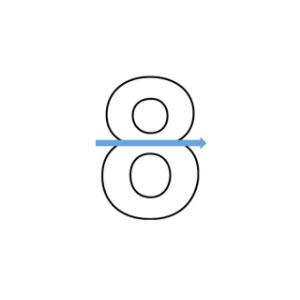
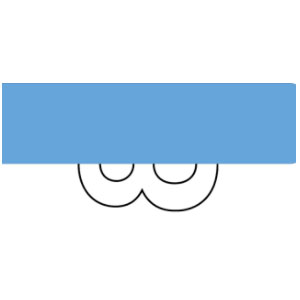
In question #1, we naturally assumed that eight was referring to the Arabic numeral used in simple arithmetic. But, how else can we see eight: 8? The Arabic numeral 8 is also a graphic image, which split horizontally gives two zeros. Half of 8 now equals zero.
Technique #2: Change the way you see the problem. We shifted 8 from a numeral to a graphic image: half of the graphic image is a circle which is the symbol for zero.
What else is ½ of 8?
Once we are seeing 8 as a graphic image, we open the doors to other ways of seeing 8. We can divide the graphic image vertically to get a skinny 3 and an awkward capital E. We can divide 8 in two diagonal directions getting a teetering “s” and a backward “s,” suitable for branding cows. Since we have changed the ways of seeing 8 and escaped unscathed, can we also manipulate the graphic image to see “w” and “m?” Turn the graphic image 8 on its side—so it looks like the infinity sign—divide it horizontally and we get a squatty “m” perched on a “w.”
Technique #3: Now, we have not only changed the way we see the problem—shifting from a numeral to a graphic image—we have also manipulated the graphic image, physically turning it to see it differently.

So far, so good. Now, try this:
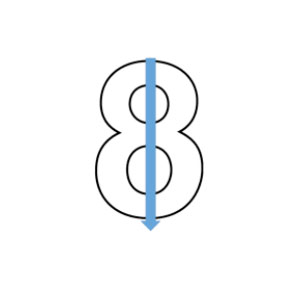
Can you see how ½ of 8 equals 6?
The natural—and perfectly reasonable—method is to continue to see 8 as a graphic image and dividing and subdividing the image with lines hoping to see the numeral 6. Since this is a blog and not a torture chamber, I can tell you that now is the time to learn:
Technique #4: At this point, we have run out of ideas about the graphic image (or at least I have.) We have been changing the way we see 8. Often we become stymied because we keep looking at the problem the same way. Problems are like mountains—you can’t move them. You can only change your position to change your view of the problem. Let’s consider how we can change our view of the problem—1/2 of 8 equals 6—to see the problem differently.
There are several ways we can change our view by restating or rewriting the problem. For example, “how does half of eight equal six.” We have shifted from Arabic numerals to English words. We could try dividing the word “eight” vertically and horizontally like we did the numeral 8.

I don’t see a solution. So, change the way you see it again. What else is 8?
You can express 8 by drawing 8 even slashes. Or, you can think of eight as a phoneme and find a homonym such as “ate.”
 It may seem that we have slipped into silliness, but you never know what may trigger your imagination to see a solution or a path to a solution.
It may seem that we have slipped into silliness, but you never know what may trigger your imagination to see a solution or a path to a solution.
For example, in 1916, an early blooming wild flower—the trailing arbutus with its red backed leaves—made Charles Kettering and Thomas Midgely, Jr. wonder if the color red would make automobile fuel detonate earlier in the cylinder, eliminating post-ignition knock. Searching for a red dye, Midgely found only a bottle of iodine. It worked, but not because it was red.
Archimedes supposedly realized the principles of water displacement in the bath tub and leapt out to tell the world.
Leaping the fence to change your view of a problem is helpful. What if you could approach your problem like Darwin or Newton or Einstein? How would Archimedes see this problem—half of eight equals six?
It would be easy for Archimedes: he’d see the problem in Roman numerals: VIII. Split it vertically as a graphic image and half of eight equals six (or two.)
(Archimedes lived in the multi-lingual port of Syracuse, Sicily and likely spoke Sicilian, Latin as well as his native Greek. He traveled to Alexandria, Egypt to study and he was killed by a Roman soldier when Rome conquered Syracuse near the end of the third century BCE.)
And, that’s the end of game day. You’ve earned your valuable participation medal. Whether you saw the answers or not is irrelevant and certainly not a measure of your “creativity” or problem solving ability. What is important is to adapt the techniques including don’t shy away from the obvious and change the way you see the problem.
(I want to thank Abe Goldstein, the great mind and accordionist of Des Moines, for showing me this puzzle back in the early 1980s.)
Save
Save
Save





